Научные и прикладные результаты лаборатории 11
2024 г.
Моделирование субволновых решеток с использованием разложения на цилиндрические волны
(совместно с ИФП СО РАН им. А.В. Ржанова)
Численно рассчитано распределение ближнего магнитного поля вокруг субволновых цилиндров различными методами (COMSOL Multiphysics, метод дискретных диполей). Расчет выполнен также методом разложения на цилиндрические волны. Установлено, что распределения интенсивности качественно совпадают. Обнаружено, что тонкие цилиндры рассеивают излучение независимо друг от друга, но взаимодействие цилиндров усиливается с увеличением их диаметра. Показано, что разложение позволяет эффективно моделировать рассеяние света и распределение полей. Результаты применимы для оптимизации метаматериалов и анализа периодических наноструктур.
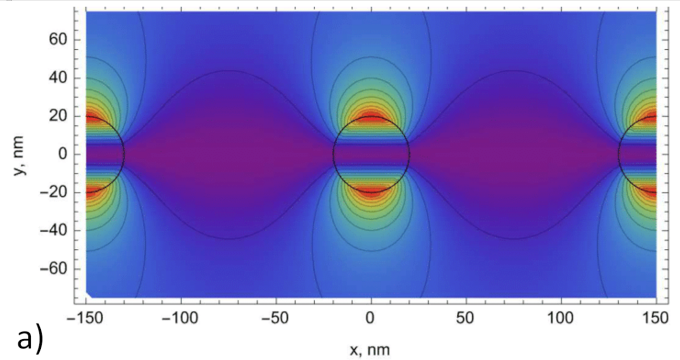 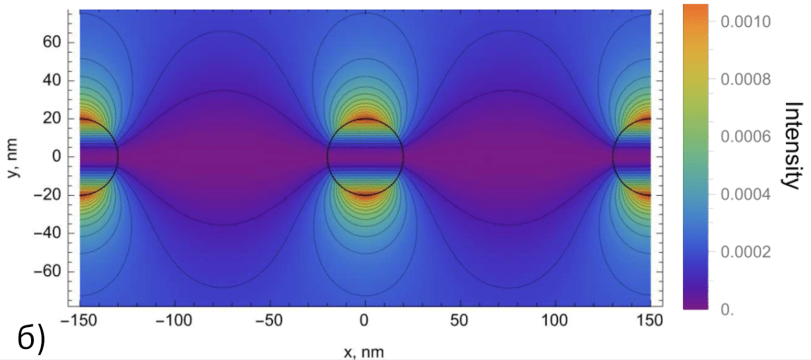
Рис.1. Распределение интенсивности рассеянного магнитного поля вблизи решетки при показателе преломления n = 1.5, длине волны λ = 1.512 мкм, радиусе цилиндра a = 20 нм, периоде L = 150 нм, полученное разложением на цилиндрические волны (а) и в среде COMSOL (б).
- Берёза А.С., Чернявский А.Е., Перминов С.В., Шапиро Д.А. Анализ распределения интенсивности ближнего поля в субволновых решетках в субволновых решетках с помощью разложения на цилиндрические волны // Квантовая электроника. - 2024, Т.54, №7, стр. 456-460.
- Берёза А.С., Чернявский А.Е., Перминов С.В., Шапиро Д.А. Рассеяние цилиндрической волны массивом круговых цилиндров // Тезисы докладов XI Международного семинара по волоконным лазерам (Новосибирск, 19-25 августа 2024 г.), Новосибирск, НГУ, 2024, стр. 141-142. [ DOI ]
2023 г.
Применение метода Римана-Гильберта и теории возмущений для решения задачи рассеяния на периодической структуре
Решена задача о рассеянии на решетке проводящих лент при нормальном падении. Была найдена система уравнений для поля с помощью метода Римана-Гильберта. Определен смысл константы интегрирования, что позволило избежать итераций. Предложены оптимальные значения удерживаемого количества гармоник для максимальной точности вычислений и рассчитаны коэффициенты пропускания. Получены выражения для интенсивности ближнего поля при рассеянии излучения субволновой решеткой, состоящей из диэлектрических цилиндров. Поле находится в виде ряда Фурье, гарантирующего периодичность. Построена теории возмущений и найдены формулы для поправки первого порядка. Результаты проверены путем сравнения с численными расчетами.
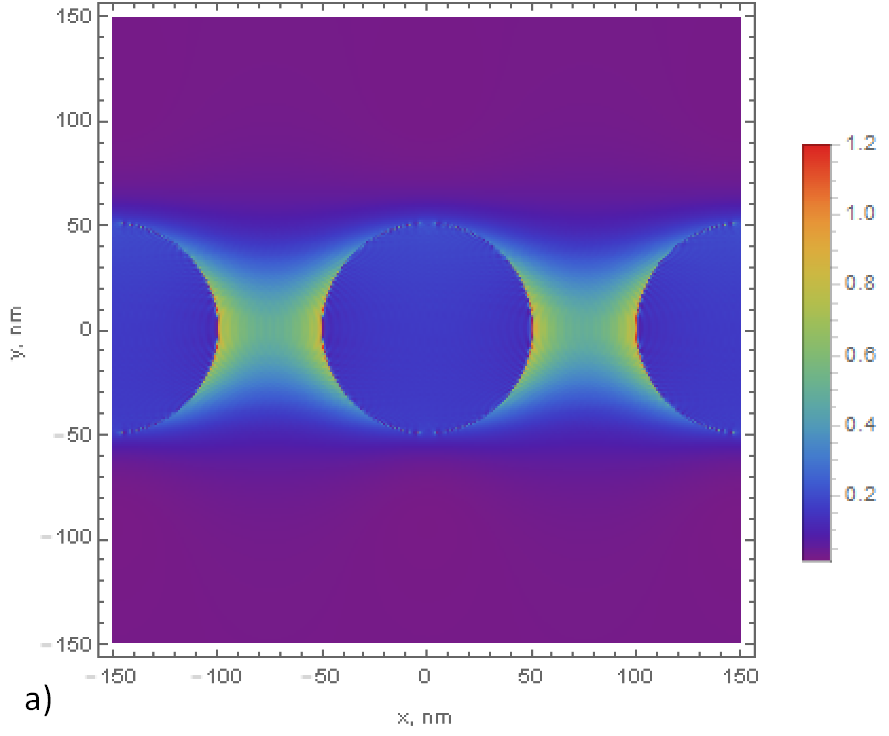 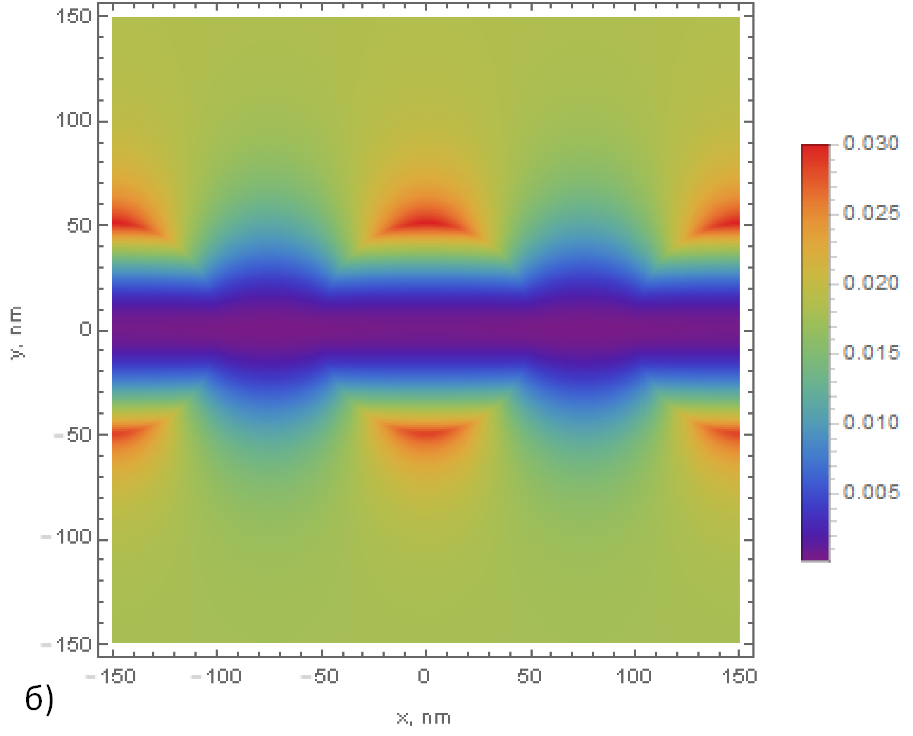
Рис.1. Распределения интенсивности рассеянного электрического (а) и магнитного поля (б) вблизи решетки при показателе преломления n = 1.5, длине волны λ = 1.512 мкм, радиусе цилиндра a = 50 нм, периоде L = 150 нм в рамках теории возмущений первого порядка.
- Nemykin A.V., Shapiro D.A. Diffraction on a Perfectly Conducting Ribbon Grating // Bulletin of the Lebedev Physics Institute. – 2023, V.50, Suppl.3, pp.S355–S365.
- Chernyavsky A., Bereza A., Frumin L., Shapiro D. Modeling of Subwavelength Gratings: Near-Field Behavior // Photonics. – 2023, V.10, No1332, 12 p.
2022 г.
Резонансное поглощение плазмонным цилиндром возле границы диэлектрика
(совместно с ИФП СО РАН им. А.В. Ржанова)
Найдено обобщение приближения дискретных диполей, позволяющее решить задачу рассеяния на металлической частице возле границы двух диэлектриков. Найден двумерный тензор Грина, который точно учитывает граничные условия. На рис. 1 изображена угловая диаграмма интенсивности локального поля на поверхности металлического цилиндра. Метод точечных диполей работает недостаточно точно вблизи границы из-за дискретности разбиения на диполи. Поэтому выполнены расчет на трех расстояниях от металла и экстраполяция на границу. В случае субволнового диаметра граница раздела может быть заменена зеркально отраженным диполем. Показано, что соответствующее аналитическое приближение обеспечивает хорошие оценки основных свойств резонанса [1]. Метод хорошо подходит для исследования металлической частицы на диэлектрической подложке.
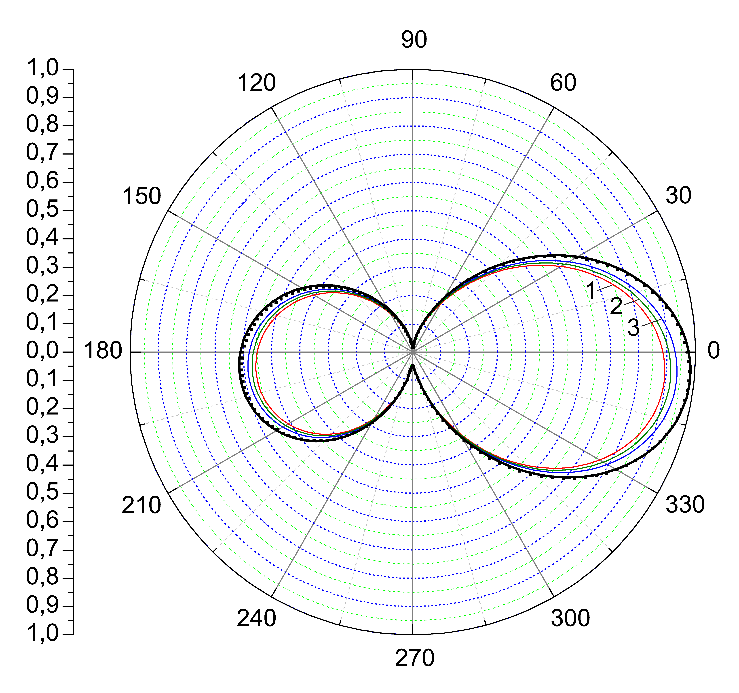
Рис.1. Полярная диаграмма рассеянного магнитного поля, рассчитанная вдоль концентрических окружностей в плоскости, ортогональной оси цилиндра. Тонкие кривые 3, 2 и 1 соответствуют рассеянному полю на радиусах 104, 106, 108 нм соответственно. Толстая кривая представляет их квадратичную экстраполяцию на радиус 100 нм (выполняется независимо для каждого значения полярного угла). Точки показывают результат метода граничных элементов.
Perminov S.V., Shapiro D.A. Resonant absorption of plasmonic cylinder near boundary between dielectrics // Phys. Letters A. – 2022, V.447, P.128295. [ DOI ]
2021 г.
Эффективный метод решения нелинейного векторного уравнения Шредингера
Разработан численный метод решения задачи Коши для нелинейного векторного уравнения Шредингера (модель Манакова), учитывающего, наряду с дисперсией и нелинейностью, еще и поляризацию волн. Метод основан на новых векторных алгоритмах решения обратной и прямой Задач Рассеяния (ЗР) для системы Манакова. Новая структура 4-блочных матриц, с векторными матрицами в недиагональных блоках, позволила обобщить известные скалярные алгоритмы. Обратная ЗР сводится к обращению алгоритмом типа Левинсона системы вложенных блочных матриц дискретизованных интегральных уравнений Гельфанда–Левитана–Марченко. Теплицева симметрия системы резко ускоряет расчеты: алгоритм требует всего O(N2) арифметических операций, где N – размер сетки. Обращение шагов алгоритма решения обратной задачи решает прямую ЗР. Численные тесты подтвердили эффективность новых векторных алгоритмов. Примером решения задачи Коши служит расчет столкновения ортогонально поляризованных солитонов Манакова (Рис. 1). Система Манакова возникает также при описании движения ультракоротких поляризованных оптические импульсов в резонансной среде. Новый метод пригоден и для этой важной задачи нелинейной оптики.
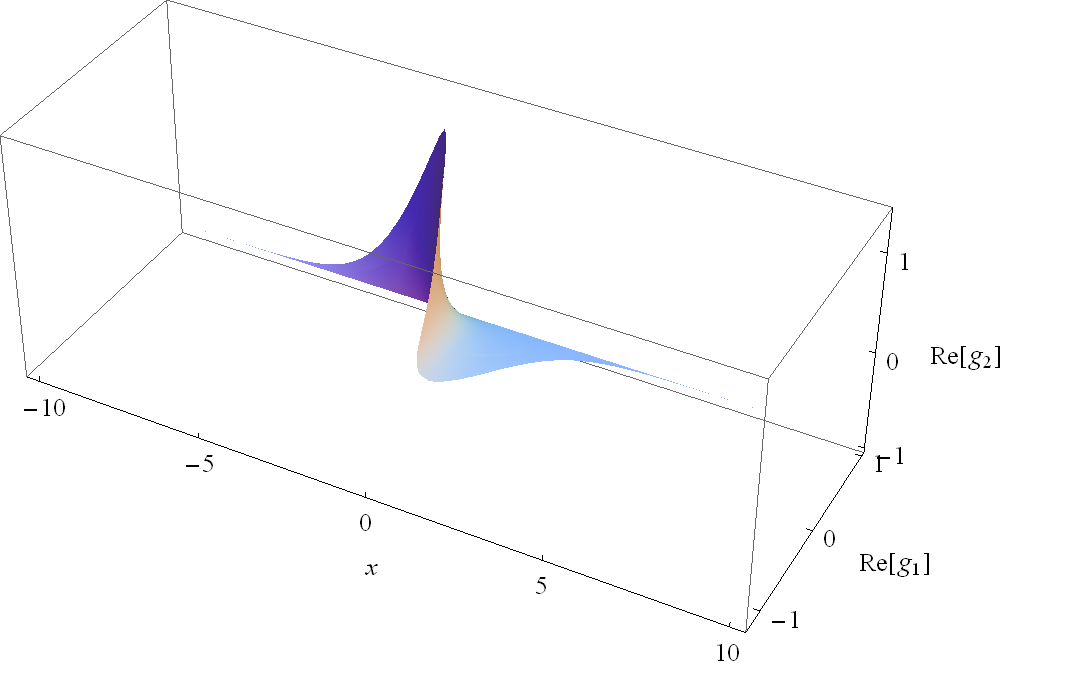
Рис.1. Расчет столкновения двух ортогонально поляризованных солитонов Манакова.
Frumin L.L. Algorithms for solving scattering problems for the Manakov model of nonlinear Schrödinger equations // Journal of Inverse and Ill-posed Problems – 2021, V.29, No.3, pp.369-383. [ DOI ]
2019 г.
Теория возмущений в задаче рассеяния света на диэлектрических телах
(совместно с ИФП СО РАН им. А.В. Ржанова)
Можно построить теорию возмущений, считая поле в свободном пространстве примерно равным невозмущенному полю падающей волны. Это приближение работает, если показатель преломления объекта близок к показателю среды. Такая ситуация типична, например, для биологических объектов в воде. Аналогичное приближение используется в квантовой механике для построения борновского ряда. Однако квантовомеханический ряд не дает корректного решения уравнений Максвелла для тел с резкой границей, потому что не соблюдаются граничные условия (скачки производной поля).
Построен ряд теории возмущений для задачи рассеяния электромагнитной волны на параллельных цилиндрах. Выведена система интегральных уравнений, точно учитывающая граничные условия на поверхности. Интегральные уравнения обобщены на случай нескольких тел произвольного сечения. Получен борновский ряд для продольной и поперечной поляризаций волны. Установлено, что в случае одного цилиндра ряд сходится к известному аналитическому решению. Сравнение с численным расчетом для двух цилиндров показало, что в третьем порядке погрешность индикатрисы рассеяния меньше 1%, рис.1. Предложенный метод позволяет получать простые аналитические формулы для сечений рассеяния света на наночастицах, которые полезны для оптической диагностики наноструктур, в частности, для анализа зависимости интенсивности рассеяния от параметров волны и диэлектрической частицы.
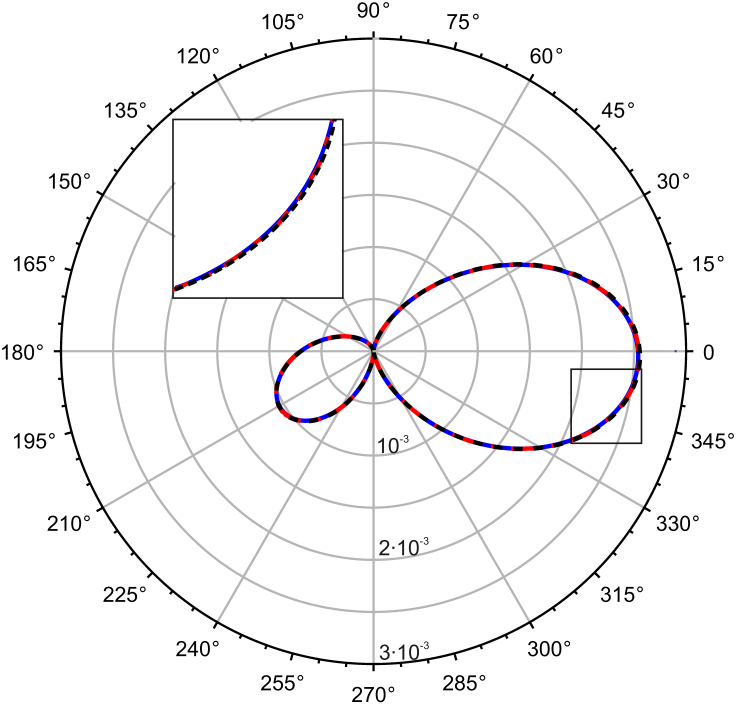
Рис.1. Угловая диаграмма рассеяния плоской э/м волны с λ = 1.5 мкм на двух одинаковых параллельных стеклянных цилиндрах с радиусами 0.1 мкм, зазор между цилиндрами 0.1 мкм, угол плоскости с осями цилиндров составляет 450 от волнового вектора (горизонта), расстояние от точки наблюдения до оси одного из цилиндров 3 мкм: 3-е борновское приближение (черная пунктирная), BEM (синяя сплошная), DDA (красная пунктирная).
- Bereza A.S., Nemykin A.V., Perminov S.V., Frumin L.L., Shapiro D.A. Light scattering by dielectric bodies in the Born approximation // Physical Review A. – 2017, V.95, p.063839.
- Немыкин А.В., Берёза А.С., Шапиро Д.А. Теория возмущений в задаче рассеяния света на диэлектрическом теле // Письма в ЖЭТФ – 2018, Т.108, №9. стр.613-617.
- Bereza A.S., Frumin L.L., Nemykin A.V., Perminov S.V., Shapiro D.A. Perturbation series for the scattering of electromagnetic waves by parallel cylinders // EPL (Europhys. Lett.) – 2019, V.127, p.20002.
2016 г.
Поле у входа в субволновую щель
Совместно с Физико-техническим институтом, Брауншвейг (Германия)
Недавно была предсказана светоиндуцированная сила между металлическими телами. Подготовка эксперимента требует расчета оптического поля между двумя проводящими плоскостями, который до сих пор не был выполнен. В данной работе задача решена для идеального металла. Найдена переходная кривая между хорошо известными предельными случаями широкой и узкой щели по сравнению с длиной волны. Показано, что кривая содержит осцилляции, вызванные рождением в щели новых волноводных мод.Для случая субволновой щели найдены простые асимптотические формулы. Теоретическая кривая хорошо согласуется с численным расчетом для золота, см. рис. 1. Исследование плазмонной силы притяжения открывает возможность практических приложений, в частности, в манипуляции микронными металлическими частицами и в технике микропереключателей.
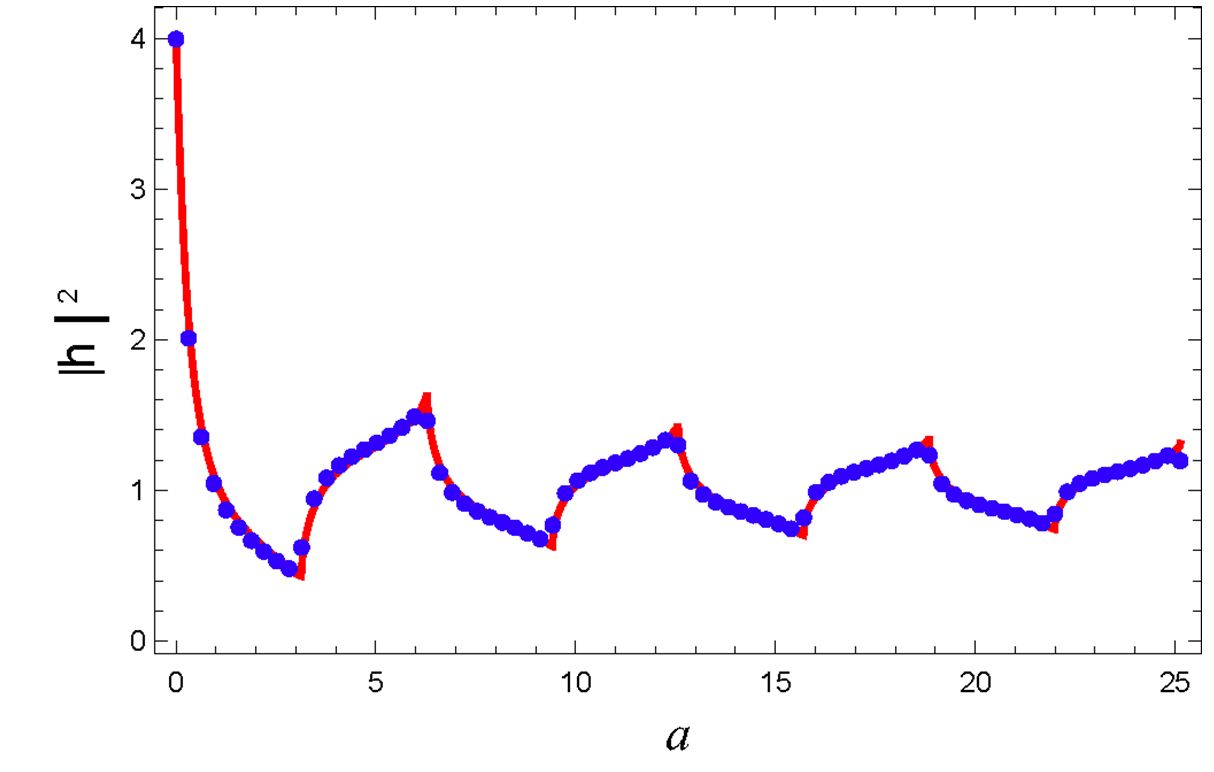
Рис.1. Теоретическая переходная кривая для идеального металла с учетом 100 пространственных мод (сплошная кривая) и численный расчет программой JCMsuite для золотой пленки толщиной 100 нм на длине волны 1.5 мкм (точки). Совпадение кривых свидетельствует о применимости модели идеального металла.
David Shapiro, Daniel Nies, Oleg Belai, Matthias Wurm and Vladimir Nesterov. Optical field and attractive force at the subwavelength slit // Optics Express – 2016, V.24, No.14, pp.15977–15982.
|











