2023 г.

Применение метода Римана-Гильберта и теории возмущений для решения задачи рассеяния на периодической структуре

Решена задача о рассеянии на решетке проводящих лент при нормальном падении. Была найдена система уравнений для поля с помощью метода Римана-Гильберта. Определен смысл константы интегрирования, что позволило избежать итераций. Предложены оптимальные значения удерживаемого количества гармоник для максимальной точности вычислений и рассчитаны коэффициенты пропускания. Получены выражения для интенсивности ближнего поля при рассеянии излучения субволновой решеткой, состоящей из диэлектрических цилиндров. Поле находится в виде ряда Фурье, гарантирующего периодичность. Построена теории возмущений и найдены формулы для поправки первого порядка. Результаты проверены путем сравнения с численными расчетами.

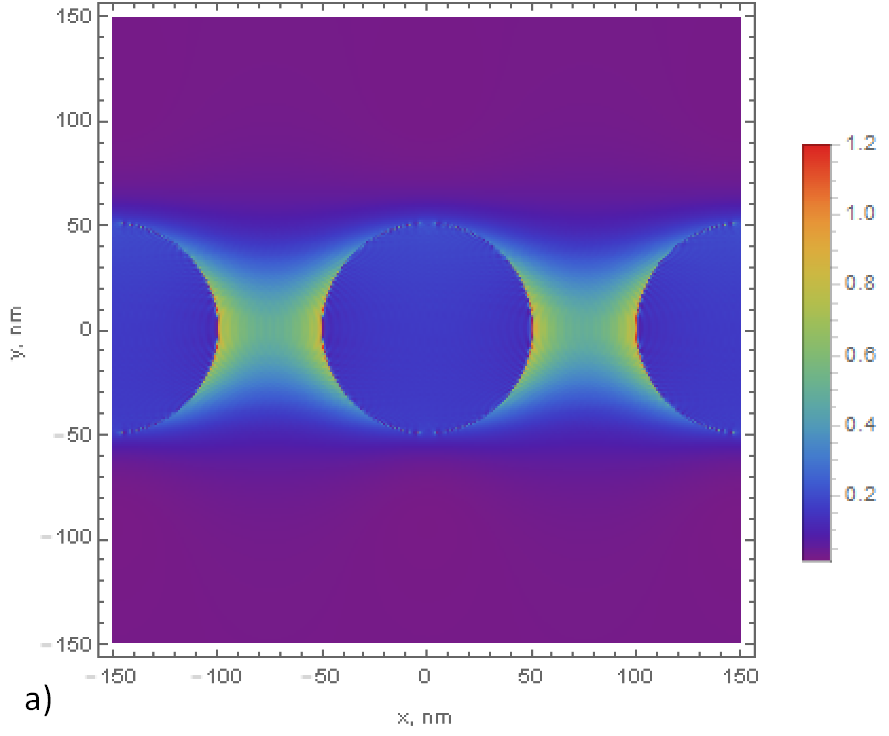
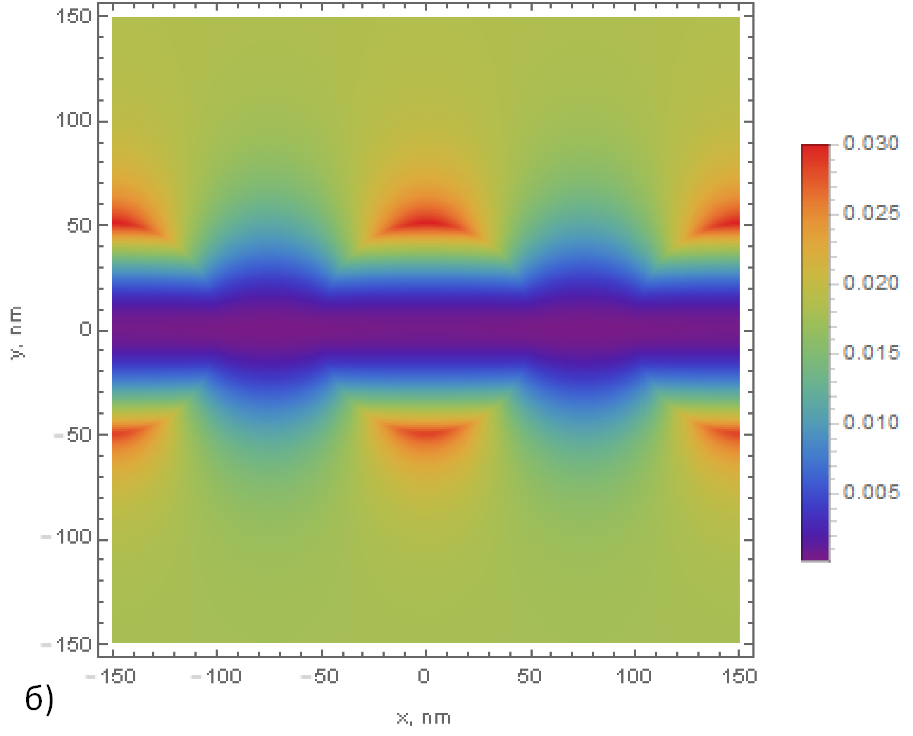
Рис.1. Распределения интенсивности рассеянного электрического (а) и магнитного поля (б) вблизи решетки при показателе преломления n = 1.5, длине волны λ = 1.512 мкм, радиусе цилиндра a = 50 нм, периоде L = 150 нм в рамках теории возмущений первого порядка.

1. Nemykin A.V., Shapiro D.A. Diffraction on a Perfectly Conducting Ribbon Grating // Bulletin of the Lebedev Physics Institute. – 2023, V.50, Suppl.3, pp.S355–S365.
2. Chernyavsky A., Bereza A., Frumin L., Shapiro D. Modeling of Subwavelength Gratings: Near-Field Behavior // Photonics. – 2023, V.10, No1332, 12 p.